What is a Derivative? - CalculusHelp

Their use in Mathematics

The use of derivatives during the study of calculus is common. It is used to measure how a function changes when the input data is changed. More simply stated, it is how much a quantity changes at any given point in the process. Line graphs are common ways to display the information gathered and to easily show the change in the data. Calculus and pre-calculus depend greatly on this study to perform some of their essential formulas.

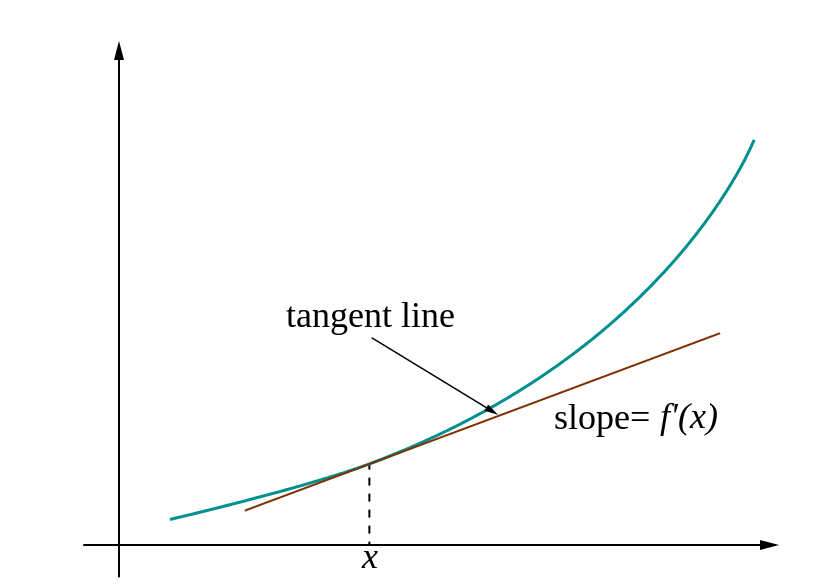
The concept of derivative is tightly related to the idea of rate of change. Indeed, a derivative measures what mathematicians like to call “instantaneous rate of change”. This idea tries to assess the limiting behavior of the change in the dependent variable y cause by a small change in the independent variable x (and by seeing what happens as the change in x becomes smaller and smaller).

Differentiation

This is the name given to the method used to measure the rate a quantity will change in relation to the change of another quantity. The rate of this change is known as the derivative. There are many complicated formulas that are used by mathematicians to calculate this change. Many of these changes can be shown on a line graph as both quantities being evaluated are real numbers. The change can be determined based on the slope of the change between the two lines.

Uses

Derivatives are common in many work place settings. Many computer programmers use them on a daily basis as a way to determine what will happen if they execute a program a certain way. Economic analysts use derivatives to help them understand the consequences of economic factors to the living situations of the people. This can prove to be vital information for determining the effect of many economic indicators.